Was ist ein Konfidenzintervall?
Wenn Sie in der Statistik eine Schätzung vornehmen, egal ob es sich um eine zusammenfassende Statistik oder eine Teststatistik handelt, ist diese Schätzung immer mit einer gewissen Unsicherheit behaftet, da die Zahl auf einer begrenzten Stichprobe der zu untersuchenden Population basiert.
Nehmen wir an, es wird eine Forschungsstudie durchgeführt, um die durchschnittliche Zeit zu ermitteln, die ein Medikament benötigt, um bei einer bestimmten Krankheit im menschlichen Körper eine Heilwirkung zu erzielen. Nachdem einige kranke Patienten bis zu ihrer Genesung beobachtet wurden, wird die Dauer der Genesung aufgezeichnet und der Durchschnitt geschätzt. Da diese Schätzung auf der Grundlage begrenzter Stichprobendaten erfolgt, ist sie mit einer gewissen Unsicherheit verbunden. Ein Konfidenzintervall ist der Grad der Unsicherheit bei einer bestimmten Kennzahl von Interesse, in der Regel ein Durchschnittswert. Es gibt an, wie sicher Sie sein können, dass die Ergebnisse eines Experiments das widerspiegeln, was Sie erwarten würden, wenn es möglich wäre, Daten der gesamten Population zu erhalten.
Was ist ein Konfidenzintervall aus statistischer Sicht?
Ein Konfidenzintervall ist der geschätzte Wert einer Kennzahl zuzüglich und abzüglich der Abweichung von dieser Schätzung. Dies ist der Wertebereich, in dem Sie erwarten können, dass Ihre Schätzung liegt, wenn Sie Ihren Test mehrmals wiederholen. Wie oft die Schätzung in den Bereich fällt, hängt von dem konfigurierten Konfidenzniveau ab.
Wenn Sie ein Konfidenzintervall mit einem Konfidenzniveau von 95% konstruieren, sind Sie sicher, dass die Schätzung in 95 von 100 Fällen zwischen dem oberen und dem unteren Wert liegt, der durch das Konfidenzintervall festgelegt ist.
Ihr gewünschtes Konfidenzniveau hängt im Allgemeinen mit dem statistischen Niveau (Alpha) zusammen, das Sie in Ihrem Hypothesentest verwenden. Wenn Sie ein Alpha von 0,05 festlegen, wäre Ihr Konfidenzniveau 1 – 0,05 = 0,95 oder 95%.
Wann verwenden Sie Konfidenzintervalle?
Immer wenn Sie eine Schätzung einer Teststatistik auf der Grundlage von Stichprobendaten vornehmen, berechnen Sie das Konfidenzintervall, um die Unsicherheit darzustellen, die innerhalb der begrenzten Stichprobendaten besteht. Der Grund dafür ist, dass Stichprobenpunktschätzungen allein keine Informationen über die Variation um die Zahl herum liefern, da die Daten begrenzt sind. Konfidenzintervalle sind nützlich, um die mögliche Variation um eine Punktschätzung herum zu kommunizieren.
Berechnen eines Konfidenzintervalls
Konfidenzintervall ist die Terminologie, die am häufigsten in der Frequentistischen Statistik verwendet wird. Die meisten Statistiksoftwares liefern das Konfidenzintervall der Schätzung zusammen mit verschiedenen Statistiken, wenn Sie einen statistischen Test durchführen.
Zur Veranschaulichung der Berechnung eines Konfidenzintervalls stellen wir uns vor, dass eine Gruppe von Analysten daran interessiert ist, festzustellen, ob die auf einer bestimmten Obstplantage angebauten Äpfel groß genug sind, um an einen Online-Lebensmittelmarkt verkauft zu werden oder nicht.
- Ermitteln Sie die Anzahl der Proben (n). Die Forscher wählen nach dem Zufallsprinzip 46 Äpfel von Bäumen auf der Farm aus. Folglich ist N = 46
- Berechnen Sie den Mittelwert der Stichprobendaten.
Die Forscher fanden dann heraus, dass das mittlere(μ) Gewicht der Äpfel 86 Gramm beträgt. - Berechnen Sie die Standardabweichung(σ). Es ist ratsam, die Standardabweichung der gesamten Population zu verwenden. In vielen Szenarien ist diese Information jedoch nicht verfügbar. Wenn dies der Fall ist, kann die Standardabweichung anhand der Stichprobe mit der folgenden Formel berechnet werden –

- Legen Sie das Konfidenzniveau fest, das verwendet werden soll. Typische Marktforschungsstudien verwenden ein Konfidenzniveau von 95/99 Prozent. Nehmen wir an, die Forscher in unserem Beispiel haben beschlossen, ein Konfidenzniveau von 95 Prozent zu verwenden.
- Ermitteln Sie für das ausgewählte Konfidenzniveau den entsprechenden Z-Wert anhand der Z-Tabelle.
| Konfidenzniveau | Z |
| 80% | 1.282 |
| 85% | 1.44 |
| 90% | 1.645 |
| 95% | 1.96 |
| 99% | 2.576 |
| 99.50% | 2.807 |
Der Z-Wert ist im Wesentlichen das Intervall, dessen Fläche einer Standardnormalverteilungskurve dem festgelegten Konfidenzniveau entspricht.

Für das gewählte Konfidenzniveau von 95 Prozent ermitteln sie, dass Z = 1,960.
6. Berechnen Sie das Konfidenzintervall anhand der folgenden Formel.
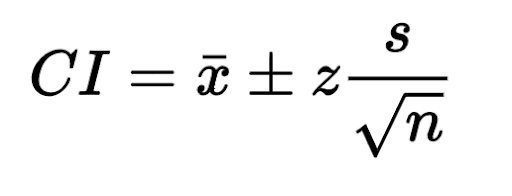
CI = 86 ± 1.960 (6.2/6.782)
Bei der Berechnung dieser Formel ergibt sich ein Konfidenzintervall von 86 ± 1,79.7. Ziehen Sie eine Schlussfolgerung
Die Forscher haben nun festgestellt, dass der Stichprobenmittelwert (41 Äpfel) wahrscheinlich (mit 95-prozentiger Sicherheit) zwischen 84,21 Gramm und 87,79 Gramm liegt. Wenn das Gewicht, das erforderlich ist, damit die Äpfel auf dem Online-Markt verkauft werden können, unter der unteren Grenze des geschätzten Konfidenzintervalls liegt, sind sie zum Verkauf zugelassen.
Vorsicht bei der Verwendung von Konfidenzintervallen
Beim Konfidenzintervall geht es nicht darum zu sagen, dass der „wahre Wert“ Ihrer Schätzung innerhalb der Grenzen des Konfidenzintervalls liegt. Die korrekte Interpretation ist, dass es eine 95%ige Chance gibt, dass das von Ihnen berechnete Konfidenzintervall den Bereich der Schätzungen enthält, den Sie erwarten, wenn Sie das Experiment mehrmals wiederholen. Mit zunehmender Datenmenge steigt die Wahrscheinlichkeit, dass Ihr Konfidenzintervall den wahren Wert Ihrer Schätzung einschließt.
Bei VWO verwenden wir die Bayes’sche Methodik, bei der wir glaubwürdige Intervalle verwenden, um die Unsicherheit um die Schätzung herum zu schätzen. Das Bayes’sche Konzept eines Glaubwürdigkeitsintervalls ist ein praktischeres und besser interpretierbares Konzept als das Konfidenzintervall. Bei einem 95%igen Glaubwürdigkeitsintervall liegt der ‚wahre Wert‘ der Metrik, die Sie schätzen wollen, mit einer Wahrscheinlichkeit von 95% im Intervall.
Um unsere Berichte im Detail zu verstehen, können Sie eine kostenlose Testversion nutzen oder eine Demo anfordern bei unseren Produktexperten .










